In this tutorial, we will learn how to use TorchProtein to solve a structure-based protein property prediction task. We will explore how to better represent the protein structure using the protein graph, and two superior protein structure encoders are employed to solve the task based on such graph representation.

• Protein Structure Data
• Dynamic Graph Construction
• Protein Structure Representation Model
• Structure-based Protein Function Prediction
  • Protein Function Prediction with GearNet-Edge

Protein Structure Data

Before defining the dataset, we need to first define the transformations we want to perform on proteins. We consider two transformations. (1) To lower the memory cost, it is a common practice to truncate overlong protein sequences. In TorchProtein, we can define a protein truncation transformation by specifying the maximum length of proteins via the max_length parameter and whether to truncate from random residue or the first residue via the random parameter. (2) Besides, since we want to use residue features as node features for structure-based models, we also need to define a view change transformation for proteins. During dataset construction, we can pass the composition of two transformations as an argument.

from torchdrug import transforms

truncate_transform = transforms.TruncateProtein(max_length=350, random=False)
protein_view_transform = transforms.ProteinView(view="residue")
transform = transforms.Compose([truncate_transform, protein_view_transform])

For the sake of efficient computation in this tutorial, we define a toy protein structure dataset EnzymeCommissionToy based on datasets.EnzymeCommission.

from torchdrug import datasets

class EnzymeCommissionToy(datasets.EnzymeCommission):
    url = "https://miladeepgraphlearningproteindata.s3.us-east-2.amazonaws.com/data/EnzymeCommission.tar.gz"
    md5 = "728e0625d1eb513fa9b7626e4d3bcf4d"
    processed_file = "enzyme_commission_toy.pkl.gz"
    test_cutoffs = [0.3, 0.4, 0.5, 0.7, 0.95]

We then instantiate a protein structure dataset based on this subclass. At the first time of instantiation, we will save a compressed pickle file enzyme_commission_toy.pkl.gz storing all the protein structure data to the local storage. The future instantiations will directly load this pickle file and are thus much faster. The Enzyme Commission dataset annotates each protein with 538 binary function labels.

import time

start_time = time.time()
dataset = EnzymeCommissionToy("~/protein-datasets/", transform=transform, atom_feature=None, 
                            bond_feature=None)
end_time = time.time()
print("Duration of first instantiation: ", end_time - start_time)

start_time = time.time()
dataset = EnzymeCommissionToy("~/protein-datasets/", transform=transform, atom_feature=None, 
                            bond_feature=None)
end_time = time.time()
print("Duration of second instantiation: ", end_time - start_time)

train_set, valid_set, test_set = dataset.split()
print("Shape of function labels for a protein: ", dataset[0]["targets"].shape)
print("train samples: %d, valid samples: %d, test samples: %d" % (len(train_set), len(valid_set), len(test_set)))

Duration of first instantiation:  414.6178753376007
Duration of second instantiation:  12.651085138320923
Shape of function labels for a protein:  torch.Size([538])
train samples: 958, valid samples: 97, test samples: 95

Dynamic Graph Construction

TorchProtein uses RDKit to construct the protein graph. The protein graph constructed from RDKit only contains four types of bond edges (i.e., single, double, triple or aromatic). Given the first sample of the dataset, let’s pick out the atoms of the first two residues and visualize the chemical bonds between them.

from torchdrug import data

protein = dataset[0]["graph"]
is_first_two = (protein.residue_number == 1) | (protein.residue_number == 2)
first_two = protein.residue_mask(is_first_two, compact=True)
first_two.visualize()

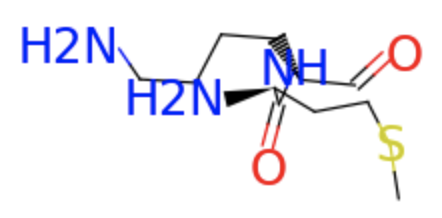
However, with bond edges alone, the rich structure information of proteins are not fully utilized. In the following steps, we seek to dynamically reconstruct the protein graph for better representing the protein structure.

Step 1: Construct Residue-level Graph

We take the first sample of the dataset as an example. For this sample, the original atom-level graph contains 2956 nodes, which is unaffordable by most structure-based models like GNNs. Therefore, in the first step, we would like to reduce the size of the graph by only retaining the nodes of Alpha carbons, which constructs a residue-level graph. We achieve this goal through the layers.GraphConstruction and layers.geometry.AlphaCarbonNode modules. layers.geometry.AlphaCarbonNode will discard those invalid residues with no Alpha carbon.

from torchdrug import layers
from torchdrug.layers import geometry

graph_construction_model = layers.GraphConstruction(node_layers=[geometry.AlphaCarbonNode()])

_protein = data.Protein.pack([protein])
protein_ = graph_construction_model(_protein)
print("Graph before: ", _protein)
print("Graph after: ", protein_)

Graph before:  PackedProtein(batch_size=1, num_atoms=[2639], num_bonds=[5368], num_residues=[350])
Graph after:  PackedProtein(batch_size=1, num_atoms=[350], num_bonds=[0], num_residues=[350])

Note. The derived residue-level graph contains no edges, since there are no two Alpha carbons connected by a chemical bond. Therefore, in the following steps, we will seek to add different types of edges to this residue-level graph.

Step 2: Add Spatial Edges

Upon the residue-level graph with no edges, we first consider adding spatial edges between the residues within a spatial distance threshold. In addition, we remove the spatial edges between the residues close with each other in the protein sequence, since these edges are less related to the folded structure. We achieve this by the layers.geometry.SpatialEdge module.

graph_construction_model = layers.GraphConstruction(node_layers=[geometry.AlphaCarbonNode()], 
                                                    edge_layers=[geometry.SpatialEdge(radius=10.0, min_distance=5)])

_protein = data.Protein.pack([protein])
protein_ = graph_construction_model(_protein)
print("Graph before: ", _protein)
print("Graph after: ", protein_)

degree = protein_.degree_in + protein_.degree_out
print("Average degree: ", degree.mean().item())
print("Maximum degree: ", degree.max().item())
print("Minimum degree: ", degree.min().item())
print("Number of zero-degree nodes: ", (degree == 0).sum().item())

Graph before:  PackedProtein(batch_size=1, num_atoms=[2639], num_bonds=[5368], num_residues=[350])
Graph after:  PackedProtein(batch_size=1, num_atoms=[350], num_bonds=[4177], num_residues=[350])
Average degree:  23.8686
Maximum degree:  51.0
Minimum degree:  0.0
Number of zero-degree nodes:  5

Note. By only using the spatial edges, there will be five nodes that are not connected to any node in the graph, which forbids messages passing through these nodes in a GNN model. In the next step, we try to address this problem by leveraging KNN edges.

Step 3: Add KNN Edges

Based on the residue-level graph above, we further consider adding KNN edges where each node will be connected to its K-nearest neighbors. Also, we will remove the KNN edges between the residues close with each other in the protein sequence. We achieve this by the layers.geometry.KNNEdge module.

graph_construction_model = layers.GraphConstruction(node_layers=[geometry.AlphaCarbonNode()], 
                                                    edge_layers=[geometry.SpatialEdge(radius=10.0, min_distance=5),
                                                                 geometry.KNNEdge(k=10, min_distance=5)])

_protein = data.Protein.pack([protein])
protein_ = graph_construction_model(_protein)
print("Graph before: ", _protein)
print("Graph after: ", protein_)

degree = protein_.degree_in + protein_.degree_out
print("Average degree: ", degree.mean())
print("Maximum degree: ", degree.max())
print("Minimum degree: ", degree.min())
print("Number of zero-degree nodes: ", (degree == 0).sum())

Graph before:  PackedProtein(batch_size=1, num_atoms=[2639], num_bonds=[5368], num_residues=[350])
Graph after:  PackedProtein(batch_size=1, num_atoms=[350], num_bonds=[5532], num_residues=[350])
Average degree:  31.6114
Maximum degree:  66.0
Minimum degree:  2.0
Number of zero-degree nodes:  0

Note. In this case, there are no zero-degree nodes any more. However, both spatial and KNN edges neglect the edges between the residues close with each other in the protein sequence. To supplement such missing information, we next consider adding sequential edges.

Step 4: Add Sequential Edges

Based on the residue-level graph above, we further consider adding sequential edges where two residues within a sequential distance threshold will be connected to each other. We achieve this via the layers.geometry.SequentialEdge module.

graph_construction_model = layers.GraphConstruction(node_layers=[geometry.AlphaCarbonNode()], 
                                                    edge_layers=[geometry.SpatialEdge(radius=10.0, min_distance=5),
                                                                 geometry.KNNEdge(k=10, min_distance=5),
                                                                 geometry.SequentialEdge(max_distance=2)])

_protein = data.Protein.pack([protein])
protein_ = graph_construction_model(_protein)
print("Graph before: ", _protein)
print("Graph after: ", protein_)

degree = protein_.degree_in + protein_.degree_out
print("Average degree: ", degree.mean())
print("Maximum degree: ", degree.max())
print("Minimum degree: ", degree.min())
print("Number of zero-degree nodes: ", (degree == 0).sum())

Graph before:  PackedProtein(batch_size=1, num_atoms=[2639], num_bonds=[5368], num_residues=[350])
Graph after:  PackedProtein(batch_size=1, num_atoms=[350], num_bonds=[7276], num_residues=[350])
Average degree:  41.5771
Maximum degree:  76.0
Minimum degree:  12.0
Number of zero-degree nodes:  0

Overview: Represent Protein Structure as Relational Graph

After such graph construction, we have represented the protein structure as a residue-level relational graph. By regarding spatial edges and KNN edges as two types of edges and regarding the sequential edges of five different sequential distances (i.e., -2, -1, 0, 1 and 2) as five edge types, we derive a relational graph with 7 different edge types. Each edge is associated with a 40-dimensional edge feature which is the concatenation of the one-hot residue features of its two end nodes.

nodes_in, nodes_out, edges_type = protein_.edge_list.t()
residue_ids = protein_.residue_type.tolist()
for node_in, node_out, edge_type in zip(nodes_in.tolist()[:5], nodes_out.tolist()[:5], edges_type.tolist()[:5]):
    print("%s -> %s: type %d" % (data.Protein.id2residue[residue_ids[node_in]], 
                                 data.Protein.id2residue[residue_ids[node_out]], edge_type))

ILE -> VAL: type 1
TRP -> GLU: type 1
LEU -> GLU: type 1
VAL -> GLU: type 1
ARG -> ASP: type 1

Protein Structure Representation Model

TorchProtein defines diverse GNN models that can serve as the protein structure encoder. In this tutorial, we investigate the superior Geometry-Aware Relational Graph Neural Network (GearNet) and its extension with edge message passing (GearNet-Edge) on our toy benchmark.

GearNet

The GearNet is specifically designed to encode the residue-level relational graph defined above, whose key component is the relational message passing among different residues. In TorchProtein, we can define a GearNet model with models.GearNet.

from torchdrug import models

gearnet = models.GearNet(input_dim=21, hidden_dims=[512, 512, 512], num_relation=7,
                         batch_norm=True, concat_hidden=True, short_cut=True, readout="sum")

GearNet-Edge

The GearNet-Edge extends the vanilla GearNet by adding edge-level message passing. In specific, GearNet-Edge constructs the line graph whose nodes are the edges of the original graph, and it connects the edges that are adjacent in the original graph. On such basis, edge message passing is realized by the relational message passing on the line graph. In TorchProtein, we can define a GearNet-Edge model with models.GearNet.

gearnet_edge = models.GearNet(input_dim=21, hidden_dims=[512, 512, 512], 
                              num_relation=7, edge_input_dim=59, num_angle_bin=8,
                              batch_norm=True, concat_hidden=True, short_cut=True, readout="sum")

Structure-based Protein Function Prediction

In this part, we seek to solve the protein functional terms prediction task on the toy Enzyme Commission dataset. We employ both GearNet and GearNet-Edge to solve this task and compare their performance.

Note. This task aims to predict whether a protein owns several specific functions, in which owning each function can be expressed by a binary label. Therefore, we formulate this task as multiple binary classification tasks and seek to solve them jointly in a multi-task learning way.

Protein Function Prediction with GearNet

We first wrap the GearNet model into the tasks.MultipleBinaryClassification module that performs all the considered binary classification tasks jointly, in which an MLP prediction head is appended upon GearNet to derive all the task predictions.

graph_construction_model = layers.GraphConstruction(node_layers=[geometry.AlphaCarbonNode()], 
                                                    edge_layers=[geometry.SpatialEdge(radius=10.0, min_distance=5),
                                                                 geometry.KNNEdge(k=10, min_distance=5),
                                                                 geometry.SequentialEdge(max_distance=2)],
                                                    edge_feature="gearnet")

task = tasks.MultipleBinaryClassification(gearnet, graph_construction_model=graph_construction_model, num_mlp_layer=3,
                                          task=[_ for _ in range(len(dataset.tasks))], criterion="bce", metric=["auprc@micro", "f1_max"])

Now we can train this model. We setup an optimizer for this model, and put everything together into an Engine instance. It takes about 2 minutes to train the model for 10 epochs on this task. We finally evaluate on the validation set.

from torchdrug import core

optimizer = torch.optim.Adam(task.parameters(), lr=1e-4)
solver = core.Engine(task, train_set, valid_set, test_set, optimizer,
                     gpus=[0], batch_size=4)
solver.train(num_epoch=10)
solver.evaluate("valid")

The evaluation result may be similar to the following.

auprc@micro: 0.107835
f1_max: 0.212811

Protein Function Prediction with GearNet-Edge

We next wrap the GearNet-Edge model into the tasks.MultipleBinaryClassification module that performs all the considered binary classification tasks jointly, in which an MLP prediction head is appended upon GearNet-Edge to derive all the task predictions.

graph_construction_model = layers.GraphConstruction(node_layers=[geometry.AlphaCarbonNode()], 
                                                    edge_layers=[geometry.SpatialEdge(radius=10.0, min_distance=5),
                                                                 geometry.KNNEdge(k=10, min_distance=5),
                                                                 geometry.SequentialEdge(max_distance=2)],
                                                    edge_feature="gearnet")

task = tasks.MultipleBinaryClassification(gearnet_edge, graph_construction_model=graph_construction_model, num_mlp_layer=3, 
                                          task=[_ for _ in range(len(dataset.tasks))], criterion="bce", metric=["auprc@micro", "f1_max"])

We train the model for 10 epochs, taking about 8 minutes, and finally evaluate it on the validation set.

optimizer = torch.optim.Adam(task.parameters(), lr=1e-4)
solver = core.Engine(task, train_set, valid_set, test_set, optimizer,
                     gpus=[0], batch_size=4)
solver.train(num_epoch=10)
solver.evaluate("valid")

The evaluation result may be similar to the following.

auprc@micro: 0.126617
f1_max: 0.230981

Note. We can observe that GearNet-Edge performs better than GearNet on this toy benchmark in terms of AUPRC and F1 max. However, the performance of both models are not satisfactory, which mainly owes to the over small dataset size. We suggest users to apply these two models on the standard datasets in TorchProtein (e.g., datasets.EnzymeCommission) to better investigate their effectiveness.